A few weeks back I wrote about the idea of coincidence, or unconnected events that seem connected in some mysterious way. This idea is a lot more interesting than I originally thought, and I want to expand on it here. Those mathematicians amongst you may wish to avert your eyes since what I am about to say is (1) obvious to you, and (2) way oversimplified. Before looking at highly unlikely events, let’s look at something which seems unlikely but tums out to be pretty common.
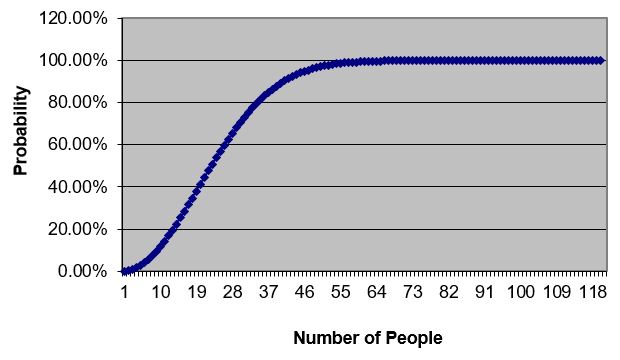
You go to a party and see that there are exactly 23 people in attendance, including you. What are the odds that any two people in the room have the same birthday? With 23 people the math says the odds are about 50/50. That result, borne out by actual experiments, runs counter to our intuition. Our linear brains would guess it should take around 183 people in the room for this to be true, since that is around 50% of the total number of possible birthdays in one year. So what is going on here? You can crank up a spreadsheet and calculate the odds of various sizes of parties (shown below), but what I find more interesting is that our brains don’t seem to handle exponential changes very well. When faced with an actual event that behaves in an exponential fashion, we are surprised at the result.
A corollary to this idea is found in Highly Unlikely Events. The idea is that given enough chances or choices, something unusual or rare is bound to happen. The best example of this idea is the lottery, you know, that thing we are sure we are going to win this time. We know that the odds of us winning are astronomical, yet the odds of someone winning are nearly certain. That is because the number of us’s is very small, and the number of someone’s is very large. That someone wins is not miraculous but a normal outcome.
The miracle for me is the way these numbers work.